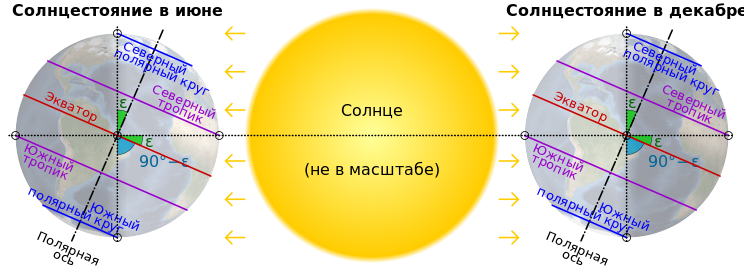
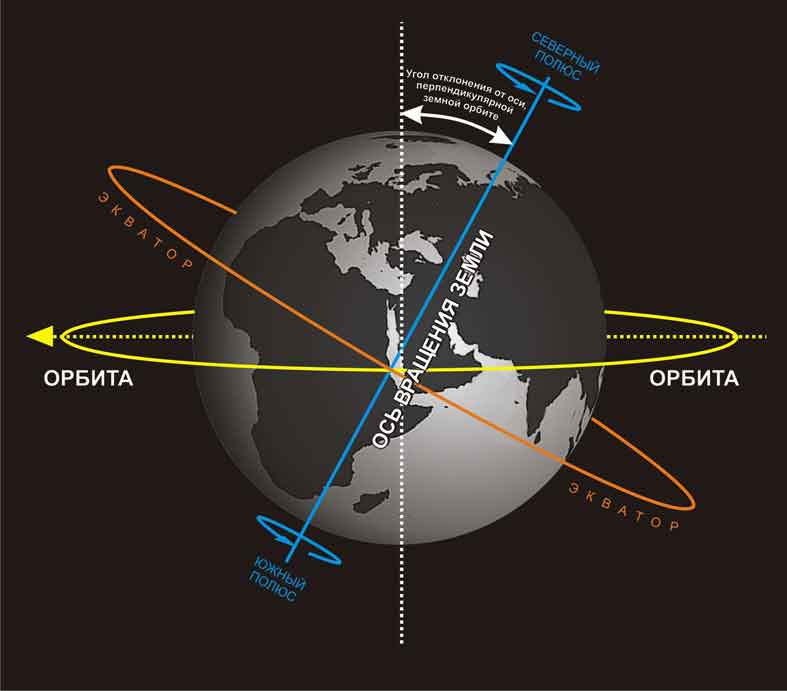
Угол наклона земной оси совпадает с широтой, Мощность солнечного излучения по регионам

Но это и не надо — во-первых, само Солнце в разных частотных диапазонах излучает с различной силой, а во-вторых, не всё, что излучило Солнце, достигает поверхности Земли — отдельные участки спектра в значительной степени поглощаются разными компонентами атмосферы — преимущественно озоновым слоем, парами воды и углекислым газом. Обычно они представляют собой плоские конструкции из тонких зачернённых трубок, уложенных в виде решётки или змейкой. Солнечные электростанции. Кубасов В. Орбитальные резонансы это когда периоды соизмеримы.
Его масштаб постоянный, а следовательно, он сохраняется во всех местах и по всем направлениям. Полное подобие изображения на глобусе с действительными земными очертаниями позволяет определять площади и расстояния, географические координаты, направления на стороны горизонта и т.
Расстояния по глобусу можно измерять тонкой металлической линейкой или натянутой нитью. Полученное расстояние в миллиметрах затем переводят по масштабу в действительные расстояния в километрах.
Нужно только следить, чтобы линейка или нить плотно прилегали к поверхности глобуса и проходили по кратчайшему пути между заданными пунктами, т. Удобно измерять расстояния по глобусу с помощью отсчетного кольца, которое можно легко изготовить самим за несколько минут.
Узкую полоску толстой бумаги склеивают в кольцо, размер окружности которого должен быть точно равен диаметру глобуса. С внешней стороны кольца на половине окружности наносят 20 делений, каждое из которых будет соответствовать км рис. Полученные интервалы делят точками на сотни километров. Чтобы измерить расстояние между какими-то пунктами, кольцо надевают на глобус и разворачивают его так, чтобы край шкалы проходил через оба пункта, причем нулевой индекс должен быть совмещен с одним из пунктов.
В таком положении отсчет по шкале против другого пункта покажет расстояние между ними. На второй половине окружности кольца нанесем градусную сетку от 0 до 90 в обе стороны от середины рис. По ней мы будем определять географическую широту пунктов. Снимем глобус с оси и наденем на него кольцо, расположив его так, чтобы край шкалы проходил через центры отверстий, на которые надевается ось, и через заданный пункт, а нулевой штрих совместился бы с линией экватора. Отсчет по шкале против пункта укажет его географическую широту рис.
Для определения долготы подклеим полоску бумаги к кольцу против нулевого штриха, как это указано на рисунке. На этой полоске нанесем градусные деления промежутка между двумя соседними меридианами по экватору, причем оцифровка их для восточной долготы должна идти справа налево, а для западной долготы наоборот. Точность определения координат зависит от масштаба глобуса: чем крупнее масштаб, тем выше точность.
Градус широты и градус долготы. Географические координаты связаны с дугами параллелей и меридианов, а их можно переводить из градусной меры в линейную и, наоборот, из линейной в градусную.
Принимая форму Земли за шар радиусом км, получим величину дуги, равную примерно км. Если два пункта находятся на одном и том же меридиане, то, определив их широты, можно узнать расстояния между ними. Значит, расстояние между городами будет равно примерно км 46,7 х Чтобы убедиться в правильности наших расчетов, определите это же расстояние по глобусу с помощью отсчетного устройства.
Что касается параллелей, то их расстояния между двумя смежными меридианами по мере удаления от экватора становятся все меньше и меньше и на полюсах принимают нулевые значения. С помощью таблицы можно решать интересные задачи, и мы будем обращаться к ней еще не раз. А сейчас, используя помещенные в ней данные, определим расстояние между пунктами, расположенными на одной и той широте. Однако это не кратчайшее расстояние между городами.
Это расстояние по параллели, а кратчайший путь пройдет значительно севернее.
Установите между ними отсчетное кольцо, и расстояние получится равным км, то есть на км меньше, чем по параллели. Как лучше пользоваться глобусом. Работать с глобусом наиболее удобно, когда он будет находиться в ориентированном положении.
Поэтому многие считают, что тем самым уже дано его ориентирование. Но это не так. Горизонтальная плоскость совпадает с плоскостью орбиты только на одной широте - на полярном круге. Здесь мы можем ориентировать глобус, направив северный конец его оси к Полюсу мира. На всех других широтах обычный глобус не ориентируется. Для того чтобы ось глобуса была параллельна оси Земли в любом месте, нужно угол наклона оси к горизонтальной плоскости сделать равным градусному значению широты этого места.
Ориентирование глобуса можно выполнить следующим образом. Установите глобус так, чтобы населенный пункт, где вы живете, был в зените, т. В таком положении подложите под основание глобуса какой-нибудь предмет, и он будет ориентрован. Впрочем, подставку вы можете сделать заранее из тре-угольного бруска.
Угол наклона на этом бруске должен соответствовать разности величины угла наклона оси глобуса и значения широты вашего населенного пункта.
А как же ориентировать глобус на экваторе и тем более в странах южного полушария? Тут уже такой подставкой не обойдешься.
Чтобы, например, определить координаты антарктических станций, нужно переворачивать глобус, придерживая его за основание. Попробуйте в таком положении выполнять на нем какие-либо измерения! В данном случае предлагаем воспользоваться следующим советом. Открутите винт, скрепляющий глобус с осью, выньте глобус и установите его на специально изготовленной подставке в виде широкого цилиндрического кольца рис.
Такую подставку можно легко и быстро изготовить из мягкого картона или толстой чертежной бумаги. Размер окружности кольца должен быть примерно равен окружности градусной параллели глобуса. Кольцевая подставка будет служить очень хорошим приспособлением для работы с глобусом в любой его части. Ориентирование глобуса на цилиндрическом кольце. Наше приспособление дает возможность произвести ориентирование глобуса для любого географического пункта. Разворачивая глобус в кольце, мы можем устанавливать его в такое положение, чтобы хорошо обозревать любой материк, любую часть акватории и выполнять в этих местах необходимые измерения.
Насколько точна модель? Учитывая соотношения 2. Часто в расчетах используют безразмерный коэффициент статического аэродинамического момента и , который вычисляется следующим образом:. Все статические коэффициенты определяются при продувках моделей в аэродинамических трубах и для каждого конкретного носителя выдаются в виде таблиц или графиков.
Допустим, что РН движется в плотных слоях атмосферы и имеет углы и , равные нулю. В этом случае, согласно 2. Пусть в какой-то момент времени мгновенно возник угол атаки , тогда сразу же появится и статический аэродинамический момент относительно оси Z 1 , равный. Ракета, которая стремится возвратиться к исходному углу атаки a под действием статического аэродинамического момента, называется статически устойчивой.
Статически устойчивая ракета всегда стремится возвратиться к нулевым исходным углам и. Если РН движется в воздушной среде и вращается вокруг ЦМ, то на нее будут действовать силы сопротивления воздушной среды, препятствующие вращению. Эти силы создают момент относительно ЦМ ракеты, всегда направленный в сторону, противоположную вращению ракеты, стремящийся уменьшить угловую скорость вращения, которая и порождает этот момент.
Данный момент называется демпфирующим моментом и обозначается M. Активный участок АУ , или участок выведения орбитального КА, предназначен для вывода аппарата на орбиту. Параметры движения в конце АУ являются начальными условиями для орбитального полета КА. Орбита КА может быть определена полностью шестью параметрами , i, P, e, , п или только общими требованиями к ней.
В качестве общих требований могут быть: время существования КА, максимальное время нахождения КА над заданными регионами земной поверхности, максимальное время пребывания в зонах повышенной радиации, ограничения на освещенность и др. Чтобы получить орбиту КА с расчетными параметрами, необходимо вывести аппарат в расчетную точку пространства с заданной величиной и направлением скорости.
Для изучения такого сложного процесса, как полет КА, необходимо правильно описать его математически, то есть при помощи системы дифференциальных уравнений с оговоренными расчетными условиями, характеризующими физическую модель движения, которая с определенной степенью точности соответствует реальному процессу. Это движение называют невозмущенным. Для удобства анализа будем рассматривать движение ЦМ РН в плоскости.
Основными силами, действующими на РН, являются: тяга двигателя Р , сила лобового сопротивления Q , подъемная сила Y и сила притяжения Земли G см. Найдем выражение для F и F n см.
Используя формулу 2. Для этого в правой части уравнения 2. В результате получаем:. Разделив переменные в 2. Рассмотрим составляющие приращения скорости, входящие в формулу 2. Преобразуем ее, используя формулы 2. Обозначив начальную массу РН в момент начала работы ступени через m 0 , а через m 1 - массу РН в конце работы ступени, заменим в 2. Проинтегрировав, получим.
Отношение - есть число Циолковского ступени. Введя понятие относительного запаса топлива ступени t ,. Эта формула дает приращение величины скорости ракеты при работе ступени в пустоте и отсутствии гравитационного поля. Поэтому с точки зрения экономии топлива угол атаки при движении РН на АУ должен быть мал по абсолютной величине.
Поэтому V G называют гравитационными потерями скорости при работе ступени и в формуле 2. Применяя теорему о среднем интегрального исчисления к 2.
С другой стороны, уменьшение t CT при сокращении запасов топлива m T ступени приводит к росту перегрузки n из-за увеличения секундного расхода топлива m c. С увеличением t CT растет относительная масса двигательной установки, и, следовательно, уменьшается относительный запас топлива ступени T.
Поэтому при выборе надо учитывать эти противоречивые факторы. Кроме того, выбор величины t CT определяется также номером ступени, предназначением РН и т. Для современных РН время работы ступени составляет с. Значит, РН должен быть не менее чем двух ступенчатой.
Характер изменения величины скорости РН на АУ показан на рисунке 2. С энергетической точки зрения выгоднее производить запуск РН в восточном направлении, т. Это окружная скорость космодрома, то есть скорость его движения вокруг оси Земли за счет суточного вращения.
На широте она равна. Каким бы образом ни была определена орбита КА - полностью или общими требованиями к ней - существует множество траекторий выведения, отличающихся программой движения РН на АУ. Определим в связи с этим требования к программе продольного движения при программе угла рыскания t 0 и программе угла крена t 0 :.
Технически наиболее простым является вертикальный старт РН. Поэтому первым участком траектории является вертикальный участок. На вертикальном участке наиболее простая программа движения. СТ -стартовый угол тангажа , и это способствует устойчивой работе автономной системы управления непосредственно после старта. Продолжительность вертикального участка составляет с. Существенно уменьшать продолжительность этого участка нельзя, так как необходимо обеспечить выход всех систем управления на устойчивый режим работы, при котором управление движением РН будет достаточно эффективным.
Таким образом, вертикальный участок удовлетворяет первому требованию к программе движения РН: осуществление технически наиболее благоприятного старта и обеспечение устойчивой работы автономной системы управления. Увеличение продолжительности вертикального участка нежелательно, так как оно приводит к росту гравитационных потерь скорости. Кроме того, при больших скоростях увеличивается программное значение нормального ускорения, необходимого для искривления траектории при заданном радиусе кривизны r:.
Следовательно, для уменьшения нормальных перегрузок необходимо искривление траектории начинать при возможно меньшей скорости, то есть по возможности раньше. Таким образом, вторым требованием к программе движения РН является ограничение нормальных перегрузок на участке начального разворота. Но при скорости РН, соответствующей 0. При 0 они вызывают нежелательные аэродинамические моменты, действующие на корпус РН. Это требование является одним из критериев при выборе программы выведения КА. Программа движения первой ступени должна обеспечить полет РН от момента старта до момента отделения ступени при удовлетворении по всей траектории движения требований, перечисленных в предыдущем параграфе.
Область определения t слева определена продолжительностью вертикального участка моментом времени t 1 , а справа - временем выключения двигателей первой ступени t к1. В результате многолетнего опыта был найден следующий вид программы:.
Рассмотрим физическую картину движения РН. РН стартует вертикально, то предусматривается небольшой по продолжительности вертикальный участок, на котором силы по нормали к траектории отсутствуют. Для искривления траектории движения РН, начиная с момента t 1 , необходимо иметь силы по нормали к траектории. С этой целью с помощью второго и четвертого рулевых двигателей см. Для этого с помощью момента замедляем вращение корпуса РН и таким образом уменьшаем угол атаки до требуемого.
Далее управляющий момент поддерживает угловую скорость РН z1 , практически равную угловой скорости поворота вектора скорости в продольной плоскости v. Траектория движения наиболее чувствительна к величине, которая рассматривается как параметр семейства программ.
Зависимость 2. Коэффициенты a и время начала разворота для данного носителя являются величинами постоянными. Поэтому программа движения t , определяемая зависимостью 2. Изменяя его значение от своего значения в сторону уменьшения, получаем семейство однопараметрических программ см.
Следует отметить, что max достигается при одном и том же времени t экстр. Варьируя параметр при работе двигательной установки ДУ первой ступени, получим семейство траекторий с различными значениями V k1 , k1 , H k1.
Чем больше max , тем сильнее будет искривлена траектория и тем меньше будет k1 и H k1. Программа движения второй ступени должна обеспечить перевод РН из состояния, определяемого параметрами движения на момент t k1 в заданное состояние орбитального полета.
Управляемое движение КА, в результате которого происходит изменение орбиты, называется маневром. Любой из перечисленных видов маневров изменяет элементы орбиты, то есть, по существу, является маневром орбитального перехода. Однако каждый вид маневра имеет свои особенности. Целью корректирующего маневра является, как это следует из названия, исправление или уточнение орбиты. Корректирующие маневры могут применяться для коррекции ошибок выведения; для коррекции элементов орбиты, изменяющихся под действием различных возмущающих факторов; для коррекции межпланетных траекторий и т.
Как правило, изменение элементов орбиты при проведении корректирующих маневров невелико. Маневры, изменяющие форму и размеры орбиты и ориентацию орбиты в плоскости, называются продольными; маневры, изменяющие положение плоскости орбиты в пространстве, - боковыми.
Если целью корректирующего маневра является изменение одного параметра орбиты, то коррекция называется однопараметрической, если двух или более - двух- или многопараметрической. Обычно при расчете параметров корректирующего маневра стремятся найти управление, требующее минимальных энергетических затрат оптимальное по критерию расхода топлива.
Это можно сделать, пользуясь выражениями для изменения элементов орбиты под действием импульсной возмущающей силы см. Данные выражения позволяют определить положение точек приложения импульсов, их величин и направлений в интересах коррекции тех или иных элементов. Так, большая полуось орбиты изменяется лишь под действием тангенциального импульса.
Следовательно, для ее коррекции нужно ориентировать вектор тяги по касательной к орбите. В этом случае для заданного значения a потребуется минимальный импульс. Коррекция эксцентриситета может осуществляться с помощью как тангенциального, так и нормального импульса. Тангенциальный импульс для коррекции эксцентриситета целесообразно прикладывать в точках апсид в зависимости от знака требуемого изменения е.
Как следует из выражения. Положение линии апсид при такой коррекции не изменится, так как второй фокус смещается по линии апсид. Рисунок 3. Наряду с тангенциальным импульсом для коррекции эксцентриситета и аргумента перигея может использоваться нормальный импульс. Из анализа выражений, приведенных в таблице 3. Из выражения следует, что нормальный импульс, приложенный в апогее или перигее орбиты, обеспечивает оптимальную коррекцию аргумента перигея.
Действительно, такой импульс смещает второй фокус по дуге окружности с радиусом ПF 2 или AF 2 см. При малых импульсах дугу можно заменить касательной и считать, что смещение происходит по перпендикуляру к первоначальной линии апсид. В результате эксцентриситет практически не изменится, а угол поворота линии апсид будет максимальным. Необходимо отметить, что, как это следует из выражений, приведенных в таблице 3.
С увеличением эксцентриситета е эта разница уменьшается. В результате все смещение переходит в изменение межфокусного расстояния, что приводит к наибольшему изменению эксцентриситета е. Для коррекции наклонения и долготы восходящего узла необходимо прикладывать к КА бинормальный импульс таким образом, чтобы он не вызывал нежелательных изменений другого элемента. Кроме того, важно, чтобы коррекция того или иного элемента производилась при минимальной потребной величине импульса, так как при этом обеспечивается минимум расхода топлива.
Если при выполнении маневра положение плоскости орбиты в пространстве не изменяется, маневр называется компланарным, если изменяется - некомпланарным.
Рассмотрим компланарные переходы. Они могут быть одноимпульсные и многоимпульсные два, три и более. Одноимпульсный переход возможен в том случае, если исходная и конечная орбиты имеют общую точку. Он осуществляется путем приложения управляющего импульса в этой общей точке точнее, в ее окрестности. Такой маневр может потребоваться при переводе аппарата с круговой орбиты на высокую эллиптическую например, для полета к Луне или на межпланетную траекторию см.
Для определения необходимого приращения скорости запишем соответствующие выражения для скорости в общей точке этих орбит. Скорость на исходной круговой орбите. Здесь V представляет собой значение характеристической скорости для одноимпульсного маневра.
С помощью характеристической скорости удобно оценивать энергоемкость маневра, так как она определяется исходя из энергетики исходной и конечной орбит, и не связана с характеристиками конкретного КА. С другой стороны, зная потребное значение характеристической скорости, можно определить как параметры маневра, так и тактико-технические характеристики КА.
Переходы между непересекающимися орбитами могут быть осуществлены путем приложения двух или более импульсов. В этом случае КА в течение определенного времени движется по переходной орбите. Схемы таких переходов весьма многочисленны и разнообразны, так как они определяются назначением маневра и параметрами исходной и конечной орбит. Маневр осуществляется следующим образом. В некоторой точке исходной круговой орбиты прикладывается касательный импульс V 1 , который переводит КА на переходную эллиптическую орбиту с апогеем, лежащим на высоте конечной круговой орбиты.
Затем в апогее переходной орбиты прикладывается касательный импульс V 2 , который переводит аппарат на конечную круговую орбиту см. Величины потребных импульсов определяются как разность между имеющейся и потребной скоростями на этих орбитах:. В этом случае импульсы V 1 и V 2 будут больше, чем при касательном переходе, однако время перехода будет меньше;. Такой переход будет еще более быстрым, но потребует большей энергетики. Предельным случаем такого перехода будет приложение радиального импульса.
Поскольку энергетика существующих КА ограничена, на практике стараются применять оптимальные в энергетическом отношении переходы. В качестве исходной и конечной орбит могут выступать и эллиптические.
На рисунке 3. На рисунок 3. Такой переход называется апсидальным переход между апсидальными точками исходной и конечной орбит , импульс направлен перпендикулярно к линии апсид. Переход между соосными эллиптическими орбитами по пересекающей переходной орбите быстрый переход изображен на рисунке 3. Переход между эллиптическими орбитами является наиболее общим случаем орбитальных переходов.
Если положения плоскостей исходной и конечной орбит не совпадают, необходим маневр поворота плоскости орбиты. Наиболее простой способ поворота плоскости орбиты заключается в приложении бинормального импульса скорости в узле начальной и конечной орбит см. Значение импульса скорости в предположении, что бинормальный импульс не меняет величину скорости, а изменяет только направление, получается из треугольника скоростей:.
Причем, чем больше скорость КА, то есть чем ниже его орбита, тем больше будет потребный импульс для поворота плоскости орбиты на заданный угол. В определенных условиях может оказаться выгодно использовать переходную эллиптическую орбиту с высоким апогеем. В этом случае маневр осуществляется следующим образом см. Первый импульс V 1 прикладывается в одном из узлов начальной и конечной орбит по касательной к исходной орбите точка П. Этот импульс переводит КА на переходную орбиту, лежащую в той же плоскости.
В апогее переходной орбиты который совпадает со вторым узлом прикладывается ортогональный импульс V 2 для поворота плоскости орбиты.
Поскольку скорость КА в этой точке значительно меньше, чем на исходной орбите, то затраты характеристической скорости на поворот плоскости орбиты будут меньше. Третий касательный импульс V 3 , приложенный в точке П, возвращает КА на исходную орбиту в новой плоскости. Такой маневр называется трехимпульсным маневром поворота плоскости орбиты.
Суммарный импульс характеристической скорости запишется в виде. Зависимость V S от этих параметров показана на рисунок 3. Несколько менее энергоемкий способ поворота плоскости орбиты состоит в разделении угла поворота на несколько частей и выполнении соответствующей последовательности трехимпульсных маневров. Однако реализация такого маневра сложна и требует больших затрат времени.
Еще один способ уменьшения энергетических затрат на поворот плоскости орбиты - применение так называемого аэродинамического или синергического маневра.
Этот маневр заключается в использовании для поворота в плоскости аэродинамических сил, возникающих при движении летательного аппарата, обладающего аэродинамическим качеством, в атмосфере. В общих чертах маневр включает четыре этапа см. За счет управления по крену осуществляется маневр в боковой плоскости. Встреча космических объектов на орбите представляет собой одну из важнейших операций в космосе, позволяющую решить целый ряд задач:.
Под операцией встречи в самом общем случае понимается выведение двух или более объектов в некоторую относительно малую область космического пространства, сближение объектов и осуществление между ними стыковки. Как можно видеть из определения, в операции встречи принимают участие, по меньшей мере, два объекта.
Один из них обычно не маневрирует пассивный. Роль пассивного объекта может выполнять орбитальная станция ОС. Активный объект маневрирующий космический аппарат будем называть транспортным кораблем ТК. R ц t , V ц t - соответственно радиус-вектор и вектор скорости орбитальной станции;. R п t , V п t - радиус-вектор и вектор скорости ТК;. Основное назначение маневра встречи состоит в том, чтобы в момент его окончания вектор q t относительного состояния двух КА, участвующих в операции встречи, принял заданное значение.
В зависимости от того, какие конечные условия требуются в момент окончания маневра t k , различают несколько видов этого маневра. В момент встречи должны обратиться в нуль только компоненты вектора относительного положения, компоненты вектора относительной скорости могут быть произвольной величины жесткий контакт :.
Процесс осуществления маневра встречи можно разделить на два этапа: вывод ТК в некоторую окрестность ОС и сближение аппаратов. Первый этап называется этапом дальнего наведения, второй - этапом ближнего наведения. Участок дальнего наведения может начинаться с промежуточной орбиты или непосредственно с участка выведения. Ближнее наведение начинается с момента обнаружения и захвата ОС бортовыми радиолокационными средствами ТК, таким образом граница между участками дальнего и ближнего наведения определяется возможностями бортовых средств.
В этом случае ТК выводится непосредственно в зону встречи. Момент запуска выбирается с таким расчетом, чтобы точка выхода ТК на орбиту попала в окрестность расчетной точки встречи. Этап дальнего наведения совмещается с выведением см. Прямое выведение ТК в зону встречи может быть компланарным и некомпланарным.
Компланарный запуск может быть обеспечен только в том случае, если орбита ОС проходит через точку старта, причем наиболее просто это можно осуществить при запуске ТК и ОС из одной и той же точки. В этом случае вывод ТК осуществляется по той же траектории.
При этом обеспечивается одновременный выход ТК и ОС в окрестность расчетной точки встречи, которая совпадает с точкой вывода ОС на орбиту. Ближнее наведение начинается сразу после окончания активного участка.
В дальнейшем условия компланарности будут выполняться через число суток, кратное знаменателю, то есть положение плоскости орбиты относительно Земли периодически повторяется с периодом Т к -n к Т ос.
Такие орбиты называются геопериодическими период обращения Земли кратен периоду обращения ОС. Эти орбиты называются минимальными геопериодическими орбитами. Таким образом, для обеспечения компланарности запуска при старте ТК из той же точки необходимо обеспечить условия геопериодичности орбит. Если условие геопериодичности орбиты ОС не выполнено или оно нарушилось вследствие возмущений при длительном нахождении ОС на орбите, период обращения ОС необходимо корректировать.
Кроме того, для выполнения условий компланарности необходимо производить запуск TK в определенный момент времени. Любое отклонение момента запуска от номинального так же, как и отклонение периода обращения ОС от геопериодического, приводит к нарушению условий компланарности см. Кроме того, при осуществлении запуска имеют место и другие ошибки и ограничения, связанные, в частности, с характеристиками ракет-носителей, поэтому практически компланарный запуск осуществить не удается.
Возникающий угол некомпланарности необходимо устранить либо на траектории выведения ТК, либо на участке ближнего выведения, что требует расхода характеристической скорости V хар.
Понятно, что чем больше ошибка во времени старта ТК, тем больше угол некомпланарности и тем больше потребный расход характеристической скорости V хар. Поэтому на отклонение момента старта ТК от минимального накладывается ограничение:. Этот интервал времени t 2 -t 1 называется интервалом или окном запуска. Величина этого интервала определяется располагаемым запасом V хар на устранение угла некомпланарности.
Маневрирование моментом старта в пределах окна запуска позволяет частично компенсировать отдельные ошибки и ограничения. Если в течение интервала запуска старт ТК не был осуществлен, располагаемый запас V хар не позволяет устранить возникший угол некомпланарности, и сближение будет невозможно.
В общем случае старт ТК может производиться и из другой точки по другой траектории. Если наклонение орбиты ОС больше широты точки старта, условия компланарности могут быть обеспечены. При этом станция в момент старта ТК может находиться в произвольной точке орбиты, поэтому траектория выведения в зону встречи должна будет включать пассивный участок. При этом время запуска ТК можно определить из выражения:. Очевидно, что для обеспечения встречи с ОС время запуска ТК, определяемое приведенной выше формулой 4.
Достижение такого равенства может быть выполнено только варьированием интервала времени t п , стоящего в правой части выражения 4. Траектория пассивного участка, а следовательно, и время движения t п на этом участке до момента начала этапа ближнего наведения будут определяться параметрами движения КА в конце активного участка.
Следовательно, меняя, например, скорость КА в конце активного участка, можно подобрать такое значение t, при котором время запуска, определяемое по формуле 4. При идеальном соблюдении условий компланарности наиболее экономичной траекторией на пассивном участке выведения ТК будет эллипс Хомана, перигеем траектории выведения является точка конца стартового участка.
Траектория выведения по эллипсу Хомана представлена на рисунке 4. Траектория 2 соответствует полному использованию энергетических возможностей РН полному выгоранию топлива. Эта область носит название области встречи. Этот вариант запуска наиболее экономичен встреча происходит при минимальном расходе топлива.
Однако время ожидания момента старта может быть велико. Рассмотрим схему выведения с активного участка с поворотом плоскости орбиты на значительный угол см. Запуск осуществляется в произвольный момент времени. При этом необходимо предусмотреть дополнительный запас V хар для устранения угла некомпланарности , причем, чем больше , тем больше требуется запас топлива. Время ожидания момента запуска при использовании этой схемы может быть значительно сокращено.
Эта схема вывода может применяться, когда требуются экстренные действия например, спасение экипажа. Для реализации схемы сближения с участка выведения орбита ОС и траектория выведения ТК должны удовлетворять целому ряду ограничений.
Кроме того, выведение по такой схеме требует достаточно больших энергетических затрат. Чтобы снять указанные ограничения и уменьшить энергетические затраты, применяют схему сближения с промежуточной орбиты.
В этом случае, как и в предыдущем, запуск может быть компланарным и некомпланарным. Схема компланарного выведения с использованием промежуточной орбиты изображена на рисунок 4. Угловое расстояние между объектами называется фазовым углом см. Задача процесса фазирования состоит в уменьшении фазового угла до заданной величины.
Транспортный корабль выводится на промежуточную орбиту - фазирующую, или орбиту ожидания, и в течение некоторого времени находится на этой орбите.
Это может быть несколько витков, сутки, несколько суток, в зависимости от принятой схемы управления. Уменьшение фазового угла происходит за счет разницы периодов обращения ТК и ОС. Здесь могут быть выделены следующие два варианта:. Тогда после соответствующего числа оборотов ТК попадает в зону встречи, то есть начальная орбита играет роль фазирующей см. Рассмотрим первый вариант см. Период обращения ТК по эллиптической орбите выражается уравнением.
Если начальное значение фазового угла 0 известно, то можно определить число полных оборотов, которые должен будет совершить ТК, прежде чем он попадет в заданный район ОС, после чего сразу начинается ближнее наведение.
Во втором варианте при фазировании на круговой орбите см. На рисунке 4. Рисунок 4. Чем больше разница высот конечной и фазирующей орбит, тем меньше число витков требуется для выполнения фазирования. В этом случае после выполнения фазирования необходимо провести маневр орбитального перехода. Как правило, этот маневр совмещается с фазированием. Очевидно, что время фазирования в этом случае возрастает почти вдвое. В настоящее время используют в процессе маневрирования несколько фазирующих орбит.
Задача этапа ближнего наведения состоит в том, чтобы вывести ТК из любой точки эллипсоида рассеивания, определяемого ошибками дальнего наведения, в ограниченную область фазового пространства для решения целевой задачи стыковка, облет и т. Дальность, на которой начинается этап ближнего наведения, зависит от имеющихся на борту ТК средств измерения параметров относительного движения и от применяемых методов сближения. Для исследования относительного движения на этапе сближения применяются различные системы координат, начала которых удобно помещать в центре масс цели, поскольку цель, как правило, совершает пассивное движение по известной орбите.
Наиболее часто употребляются следующие системы координат. Ось ОY все время направлена вдоль радиуса-вектора цели, ось ОХ нормальна к ней, лежит в плоскости орбиты и направлена против движения. Ось ОZ дополняет систему до правой см. Лучевая визирная система координат ВСК связана с "лучом" или линией визирования.
Ось ОХ направлена вдоль вектора дальности от цели до перехватчика вдоль линии визирования , ось OZ совпадает с вектором угловой скорости линии визирования лв , ось ОY дополняет систему координат до правой. Оси ОХ и ОY определяют плоскость наведения см. Эта система координат связана с линией визирования и плоскостью орбиты цели.
Ось OZ дополняет систему до правой см. Использование ВСК и ОВСК позволяет записывать уравнения относительного движения непосредственно в измеряемых параметрах , , лв , дальность, скорость сближения, угловая скорость линии визирования , что согласуется с визуальной картиной, воспринимаемой космонавтом.
Однако уравнения движения при этом получаются достаточно громоздкими. При исследовании относительного движения ТК и ОС на этапе сближения приняты следующие предположения:. Исключая R ТК при помощи выражения для D , из уравнения 4.
Опуская промежуточные выкладки, запишем следующее векторное уравнение относительного движения TK и OC:. Это уравнение удовлетворительно описывает относительное движение на сравнительно небольших дальностях до OC при продолжительности сближения до половины периода обращения OC. В уравнении 4.
На рисунок 4. Оно зависит от угла между вектором дальности и радиусом-вектором цели. Проецируя это уравнение на оси выбранных систем координат, получим системы дифференциальных уравнений, описывающих движение одного КА относительно другого. OC - угловая скорость обращения цели по орбите;. Из уравнений 4. Управление сближением осуществляется путем задания закона изменения управляющего ускорения a t или a x t , a y t , a z t. Решение систем уравнений при известных правых частях дает траекторию относительного движения.
В этом случае система дифференциальных уравнений 4. Для получения уравнения траектории возведем в квадрат и сложим уравнения 4. После ряда преобразований получим:. После этапа дальнего наведения предусматривается этап ближнего наведения и причаливания, задача которых обеспечить выполнение требуемых конечных условий в зависимости от типа задачи. Ближнее наведение реализуется бортовой системой транспортного корабля, при этом для выполнения маневрирования транспортный корабль должен иметь двигательную установку, обеспечивающую необходимые управляющие воздействия.
И в том, и в другом случае траектория сближения КА представляет собой совокупность активных и пассивных участков, а управление сближением сводится к последовательной коррекции орбитального движения, обеспечивающей выполнение заданных условий. В связи с тем что время движения на активных участках траектории существенно меньше времени движения на пассивных, при изучении закономерностей движения на этапе ближнего наведения можно воспользоваться импульсной аппроксимацией, то есть считается, что изменение скорости в результате маневра происходит практически мгновенно.
В зависимости от количества и расположения на транспортном корабле двигателей, создающих управляющие ускорения, различают два вида управления - полярное и декартовое или координатное.
Полярное управление реализуется, если транспортный корабль имеет один двигатель по продольной оси см. При декартовом управлении на транспортном корабле устанавливается шесть координатных двигателей по каждой из трех осей транспортного корабля в положительном и отрицательном направлениях см. К числу недостатков полярной схемы относится в первую очередь необходимость разворота транспортного корабля для совмещения вектора тяги двигательной установки с направлением управляющего импульса, что делает неприменимой эту схему управления на этапе причаливания, поэтому обычно на ТК применяют комбинацию полярной и декартовой схем.
Алексеев К. Маневрирование космических аппаратов. Балахонцев В. Сближение в космосе. Алёшин А. Основы теории полета космического аппарата. Кубасов В. Методы сближения на орбите. Левантовский В. Механика космического полета в элементарном изложении.
Нариманова и М. Коньшин; АУЭС. Алматы, - 78с. Учебное пособие предназначено для студентов всех форм обучения по специальностям аэрокосмического направления дисциплины: «Баллистика» и «Космические технологии» и при изучении отдельных вопросов космической связи по специальности подготовки бакалавра «Спутниковые и радиорелейные системы передачи» и магистра «Исследование технологий оказания спутниковых и радиорелейных услуг в радиоэлектронике» специальности "Радиотехника, электроника и телекоммуникации" для всех форм обучения Табл.
ББК Петров АУЭС, докт. Козин Печатается по плану издания Министерства образования и науки Республики Казахстан на г. Содержание Введение 4 1 Общие положения теории запуска спутников на орбиту 4 1. Рисунок 1.
В зависимости от места положения начала координат системы делятся на: - гелиоцентрические - с началом в центре масс Солнца; - геоцентрические - с началом в центре масс Земли; - топоцентрические - с началом координат в пункте наблюдения на поверхности Земли; - барицентрические - с началом координат в центре масс КА; - планетоцентрические - с началом координат в центре масс планет: Венеры, Марса, Юпитера и др.
Ниже приведены наиболее употребительные системы координат. Из теоретической механики известно, что сила притяжения является консервативной силой, а значит, проекции этой силы на оси прямоугольной СК O з XYZ , жестко связанной с центром масс Земли, равны частным производным от потенциала сил притяжения по соответствующим координатам: 1. Величины ускорений радиального и меридионального силы тяжести см. Сферой действия малого тела называется та область пространства, в которой выполняется условие Здесь g vb - возмущающее ускорение большого тела; g vm - возмущающее ускорение малого тела; g m - ускорение, создаваемое малым телом; g b - ускорение, создаваемое большим телом.
На границе сферы действия имеет место равенство Внутри сферы действия малое тело принимается за центральное, а большое оказывает возмущающее воздействие. Рассмотрим теперь картину гелиоцентрического движения. Тогда движение ракеты описывается дифференциальным уравнением движения точки: , где m - масса ракеты; V - вектор скорости центра масс; P - сила тяги ракетного двигателя.
Величину реактивной силы можно представить в виде: где - секундный расход массы; V r - скорость истечения продуктов сгорания из сопла ракетного двигателя. Уравнение движения центра масс ракеты примет вид Это уравнение движущейся точки переменной массы, полученное И. Следовательно, для того чтобы искусственный спутник мог двигаться вокруг притягивающего центра по круговой орбите радиуса r, он должен иметь постоянную энергию, равную значению потенциала поля тяготения на этом расстоянии Скорость, соответствующую этой энергии, называют круговой скоростью.
Из условия равновесия сил см.
Зная потребную характеристическую, можно найти потребное число Циолковского 2. Коэффициент полезной нагрузки представляет собой отношение полезной нагрузки к стартовой массе РН Полезной нагрузкой одноступенчатой РН является масса выводимого на орбиту космического аппарата. Тогда Таким образом, каждый килограмм стартового веса в первом случае используется более эффективно. Структурная характеристика РН - это отношение стартовой массы РН без полезной нагрузки к массе конструкции РН Этот коэффициент характеризует конструктивное совершенство РН или степень заполнения РН топливом.
Часто вместо структурной характеристики РН S используют коэффициент конструкции E - отношение веса конструкции РН к ее стартовому весу В настоящее время величина коэффициента конструкции E составляет 0,05 - 0,1.
Введем следующие обозначения: n - число ступеней ракеты; m n - масса полезной нагрузки; m 0 - начальная стартовая масса ракеты; m i - масса ракеты с отброшенными 1,2, После работы n-ой ступени скорость V n , сообщенная КА ракетой-носителем, будет равна или Во всех этих выражениях под знаком логарифма стоит число Циолковского для одно -, двух -,